Page d'accueil du site| Home page
Joukovski (Windows XP, Windows 7)
Generation of Joukovski airfoils

Introduction

Nikolai Joukovski (1847-1921) was a Russian scientist and a pionneer in the field  of hyro and aero dynamics. His early studies were on the Magnus effect produced by a rotating cylinder in a wind flow. In 1902 he built the first wind tunnel. He founded in 1904, near Moscow, the first aerodynamic research institute in Europe, became the famous TsAGI in December 1918 by decree of the Soviet government.

Among his many works in physics and mathematics, he is known in particular for determining the geometry of airfoils using a mathematical tool based on the conformal mapping of a circle.

While these airfoils offers very interesting properties, while at least for a range of low Reynolds numbers corresponding to the models, they seem to have been forgotten in favor of wing sections developed for real aviation. Moreover, it appears that the performances of the wing sections are directly based on the value of the Reynolds number. And an airfoil which gives excellent results on a plane or a glider with a large Reynolds number can have a catastrophic behavior on a model where the value of the chord of the wing is small and / or the speed of relative wind is low.

In fact, we do not find in the literature the coordinates of Joukovski wing sections while those of NACA, Wortmann, Eppler ... are widely available. Joukovski software calculates the coordinates of these wing sections by simply introducing the value of the relative thickness and the value of the maximum curvature of the mean line of the wing sections.

Software use

The software  Joukovski presents a main page where three data needed to compute the airfoil are introduced


Three text boxes are used to introduce initialization values. In 1, we introduce the value of the maximum curvature of the mean line of the wing section expressed in percentage of the chord. In 2, we introduce the value of the relative thickness of the wing section expressed in percentage of the chord. In  3 we introduce the generic name of the file where will be stored  coordinates of the wing section. This name must be composed of two letters and two digits (eg xx00). Note that these names and file formats are compatible with Wings 2.12, CFD, Eole and Visupro.

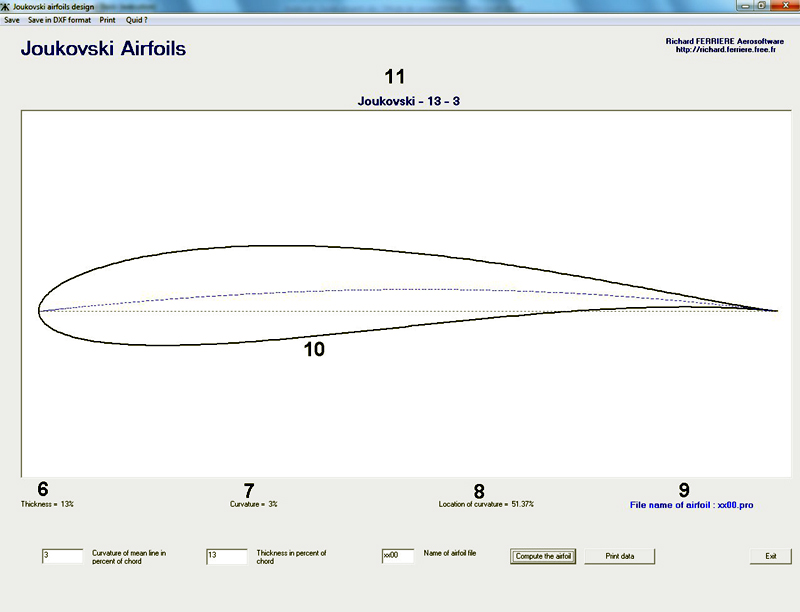
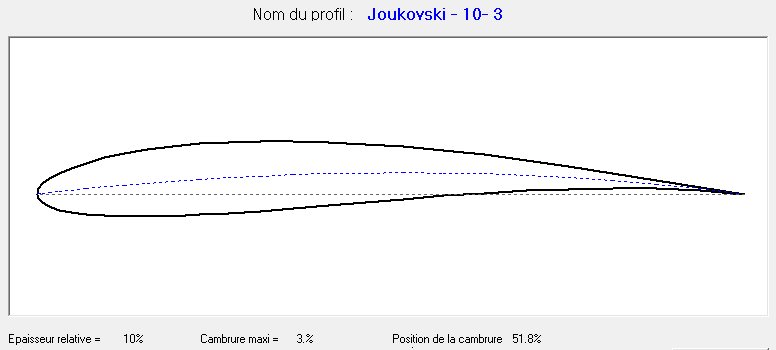
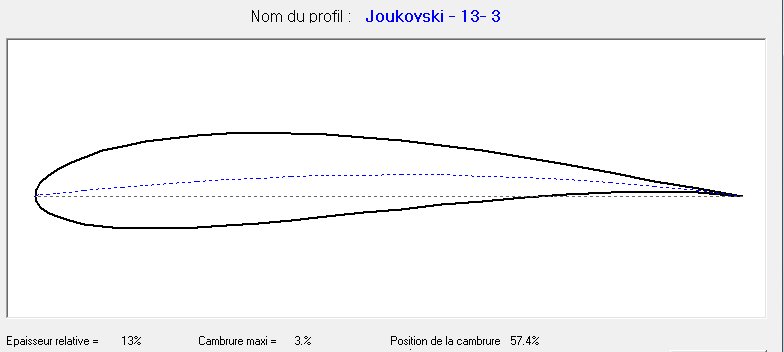
Clicking on command 4 runs the calculation of the file. The value of the relative thickness appears at 6, the curvature value at 7 and the position of the camber along the chord at 8. The name of the file containing  coordinates of the wing section at 9, the pattern of the wing section 10. Finally in 11, the profile name is indicated : it is composed by the name Joukovski, the value of the relative thickness and the maximum camber (eg: Joukovski-13-3).


At the top of the window, drop-down menus appear for recording and printing of the calculated wing section
The Save menu allows to record wing section coordinates in a ".pro" format that can be read with a text editor like NotePad for example



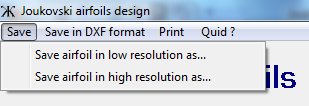
Two options are available:

- Save in "low resolution" in a ". pro"  format ( directly usable with Wings 2.12). The wing section is described by 50 dots. The wing section file is called " jk00.pro" for example

- Save in "high resolution" in a ". pro" format.  The wing section is described by 360 dots. The wing section file is called "zjk00.pro" for example, the letter z added to the name is used to distinguish between high and low resolution of wing section.

  • Save in DXF format menu allows you to record the coordinates of the calculated wing section in a ".dxf" format recognized by most of CAD softwares like Autocad, Solidworks and software control of digital milling machines


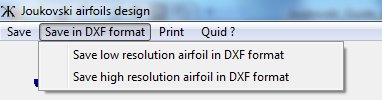
 Again two options are available to save the wing section in low and high resolution.

- One can specify the value of the chord of the wing section. By default this value is proposed to 100, it can be modified without limitation of dimensions.

- The other option is used to assign a scale factor. Default factor is 1. This factor can be modified.

  • The Print menu provides two options too.

    - Multi-format printing option to print the drawing with high resolution by setting the value of the chord of the airfoil. Its possible to choose the  printer format from A4 to A0. Moreover, if the format of the printer is less than the size of a drawing a scale reduction is requested. It is possible to adjust the line thickness of the airfoil outline, to change colour, to choose to print calculation points that define the outline, to select the copy number and the printing quality.

    - Printing multisheets, this option is for those who have only A4 printer but want to print patterns larger than the printable area for A4 "portrait". Insert the value of the airfoil chord and click on the Print command. If the chord is more large than the width of an A4 page in portrait mode, the drawing will be divided into many sheets as necessary. It will then needed to reconstruct the picture by associating the printed pages using the alignment marks.

Comparative evaluation of Joukovski airfoils performances

The choice of a wing section for a model is rarely done in a rational manner. Often we rely on the reputation of a peculiar airfoil or on a experience we had on other airplanes. This partly explains why the Joukovski airfoils are ignored in the field of model design. In fact, their properties would justify that one is interested. The range of Reynolds numbers (the Reynolds number is proportional to the product of the chord length by the relative wind speed) in which these profiles are efficient, corresponds to the values of the chords and speeds commonly used for model.

A comparative study, by the mean of CFD sofware, of airfoils with a chord equal to 250mm and relative wind speeds between 5m/s (18km/h) and 30m/s (108km/h) or 80 206 <Re <517,241 was made on Joukovski-12-3, 195 Eppler, Eppler 201. These airfoils have a thickness of approximately 12% and a maximum camber of 3% 




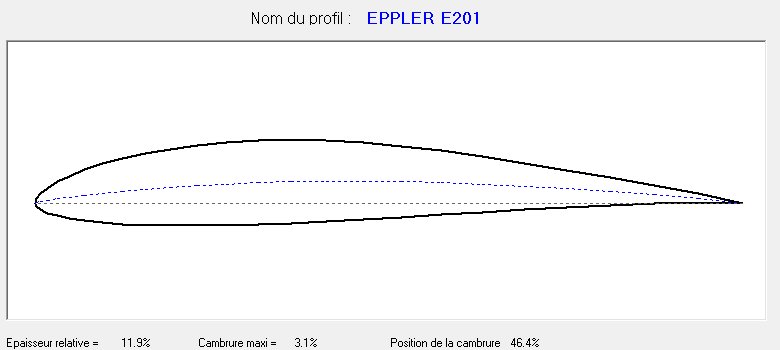
Eppler 195 and 201 airfoils are often considered as a reference by models designers

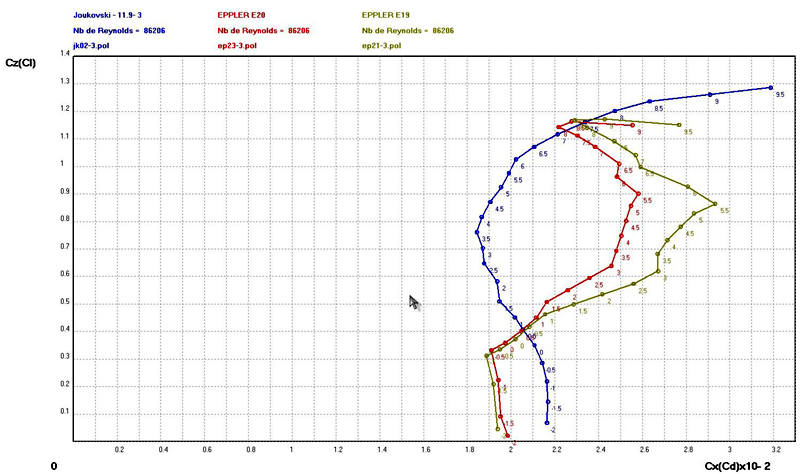
Re=80206 (chord=250mm, v=5m/s)


Re=120689 (chord=250mm, v=7m/s)


We note that, for very low speeds (5-7 m/s), Eppler 195 and 201 have an irregular polar curve with an sharp kink point at 7 ° incidence for a Cl max= 1.1. While the Joukovski polar is regular, without  inflection, and Cd min approximatively equal to  1.3. For common incidence angle, the difference of Cd values between  Joukowski and Eppler airfoils is quite high.

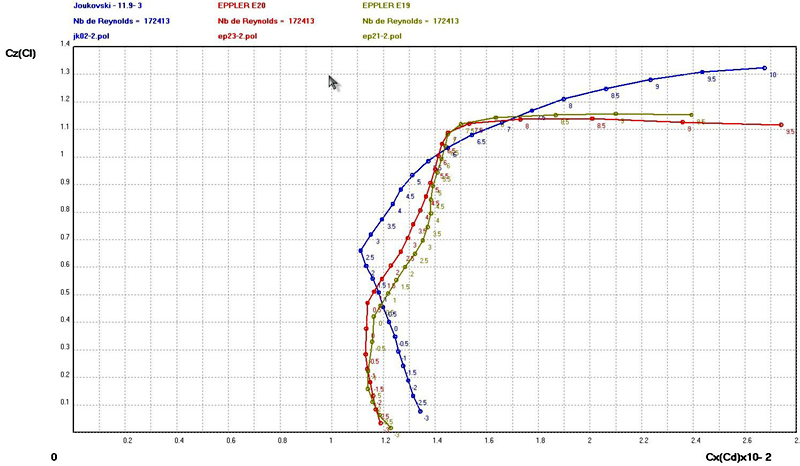
Re=172413 (chord=250mm, v=10m/s)


Re=258620 (chord=250mm, v=15m/s)


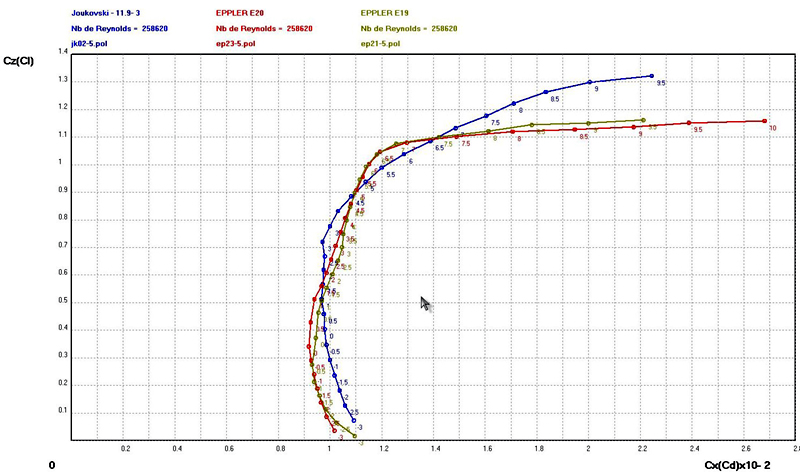
Between 10 m/s and 15 m/s, Joukovski airfoil  is better than the Eppler airfoils especially for high incidence angle

Re=344827 (chord=250mm, v=20m/s)


Re=517241 (chord=250mm, v=30m/s)

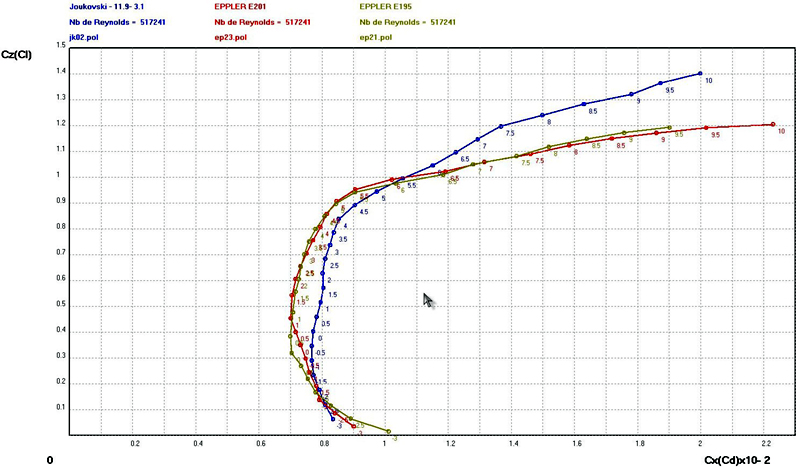
At 20 m/s the three airfoils exhibit behaviour nearly equivalent except for higher incidences where Joukovski appears better at Cl level. At 30 m/s, the Eppler airfoils (Cd ~ 0.7) are more efficient than the Joukovski (Cd ~ 0.8), which takes the advantage in terms of Cl for incidence angle above 5.5°

Conclusions :

  • Joukovski airfoils allow to fly with large speed differences.
  • The polar of these airfoils show that they are usable with high angles of incidence and offer comfortable lift coefficients.
  • The combination of the above two points indicates that they allow low speeds for takeoff and landing without risk of brutal stalling.
  • These characteristics indicate that this type of airfoil is well suited for

-       training aircraft,

-       gliders for slope soaring with slow winds,

-       towing airplanes by providing a wide  speed range

-       for motorgliders, the high lift coefficients associated with a moderate drag will offer a good rate of climb.

-       In terms of construction, rounded nose facilitates the achievement and the strength of the leading edge along the wing. They are also well suited for wings with high aspect ratio where extreme wing section works with low Reynolds number.

• Variation of the polar curve of Joukovski airfoils versus thickness  for a constant curvature value .(Re=172,413)








click to enlarge

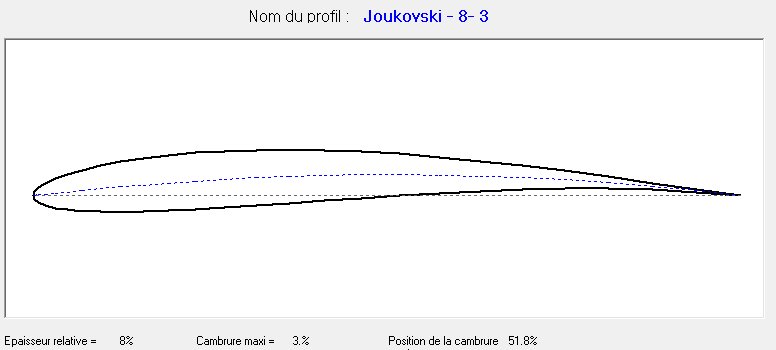
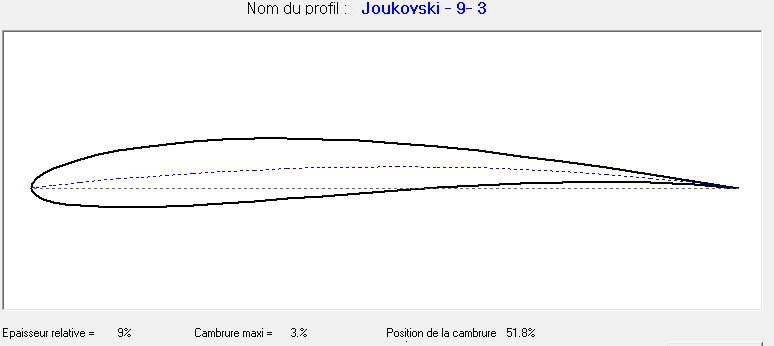
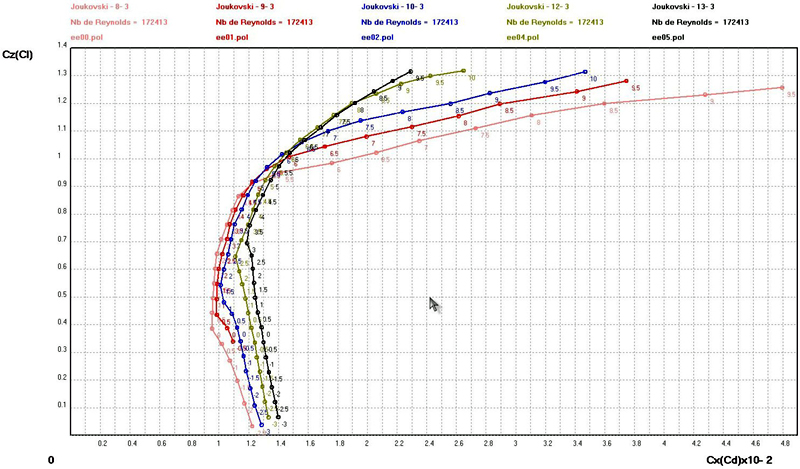
• Variation of the polar curve of Joukovski airfoils versus curvature value  for a constant thickness.(Re=172,413)